Number Converter
Mit Number Converter kannst Du eine Zahl von einem Zahlensystem der Basis 2 bis 36 in ein anderes Umwandeln. Hier geht es zur neueren und umfangreicheren Online-Version.| Programmdatei: | Number Converter.exe |
| Version: | 1.00 |
| Downloadgröße: | 33,5 KB |
| Größe auf der Festplatte: | 33,5 KB |
| Benötigte Dateien: | scint91.dll |
| Installation: | Lade die Datei herunter. |
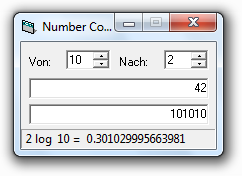
| Bedienung: | Nachdem Du das Programm gestartet hast, kannst du unter "Von" und "Nach" einstellen von und in welches Zahlensystem Du konvertieren möchtest. Möglich sind die Zahlensysteme 2 bis 36. In das obere Eingabefeld gibst Du deine Zahl ein und in dem unterem Eingabefeld siehst du das Ergebnis. Ganz unten wird der Logarithmus der beiden Zahlensysteme angezeigt. |
| Tipps: | Der Logarithmus gibt an, wie viele Ziffern im oberem Zahlensystem eine Ziffer im unterem Zahlensystem entspricht. |
Was ist ein Zahlensystem?
Normalerweise benutzen wir die Ziffer 0 bis 9. Wenn wir über 9 Zählen wollen, benötigen wir 2 Ziffern: 10. Das steht für 1 * 101 + 0 * 100. 126 Steht also für: 1 * 102 + 2 * 101 + 6 * 100.Wir können aber auch andere Zahlensysteme benutzen. Z.B. von 0 bis 15. Da wir keine Zeichen für 10, 11, usw. haben benutzen wir einfach Buchstaben: 10 = A; 11 = B; 12 = C; 15 = F; u.s.w. 2F steht für 2 * 161 + 15 * 160 = 2 * 16 + 15 * 1 = 32 + 15 = 47. Also gilt:
2F = 47
Was ist ein Logarithmus?
2 hoch wie viel ergibt 10?Schreiben wir diesen Ausdruck mathematisch, bekommen wir die Gleichung: 2X = 10
X ist die gesuchte Zahl. Um X zu bestimmen, müssen wir die Gleichung nach X auflösen. Das X steht im Exponenten. Also müssen wir das Potenzieren umkehren. Um das Multiplizieren umzukehren dividiert man. Um das Potenzieren umzukehren logarithmiert man. Unsere Gleichung sieht danach so aus:
log(2X) = log(10)
Nach dem Logarithmengesetz können wir jetzt das X aus dem Logarithmus heraus hohlen:
X * log(2) = log(10)
Danach dividieren wir die Gleichung durch log(2)
X = log(10) : log(2)
log(10) und log(2) können wir mit dem Taschenrechner ausrechnen:
X = 1 : 0,3010 = 3,3223 Folglich gilt: 10 = 23,3223